JavaScript 数据结构与算法之美 - 非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?
1. 前言
想学好前端,先练好内功,内功不行,就算招式练的再花哨,终究成不了高手。
非线性表(树、堆),可以说是前端程序员的内功,要知其然,知其所以然。
笔者写的 JavaScript 数据结构与算法之美 系列用的语言是 JavaScript ,旨在入门数据结构与算法和方便以后复习。
非线性表中的树、堆是干嘛用的 ?其数据结构是怎样的 ?
希望大家带着这两个问题阅读下文。
2. 树
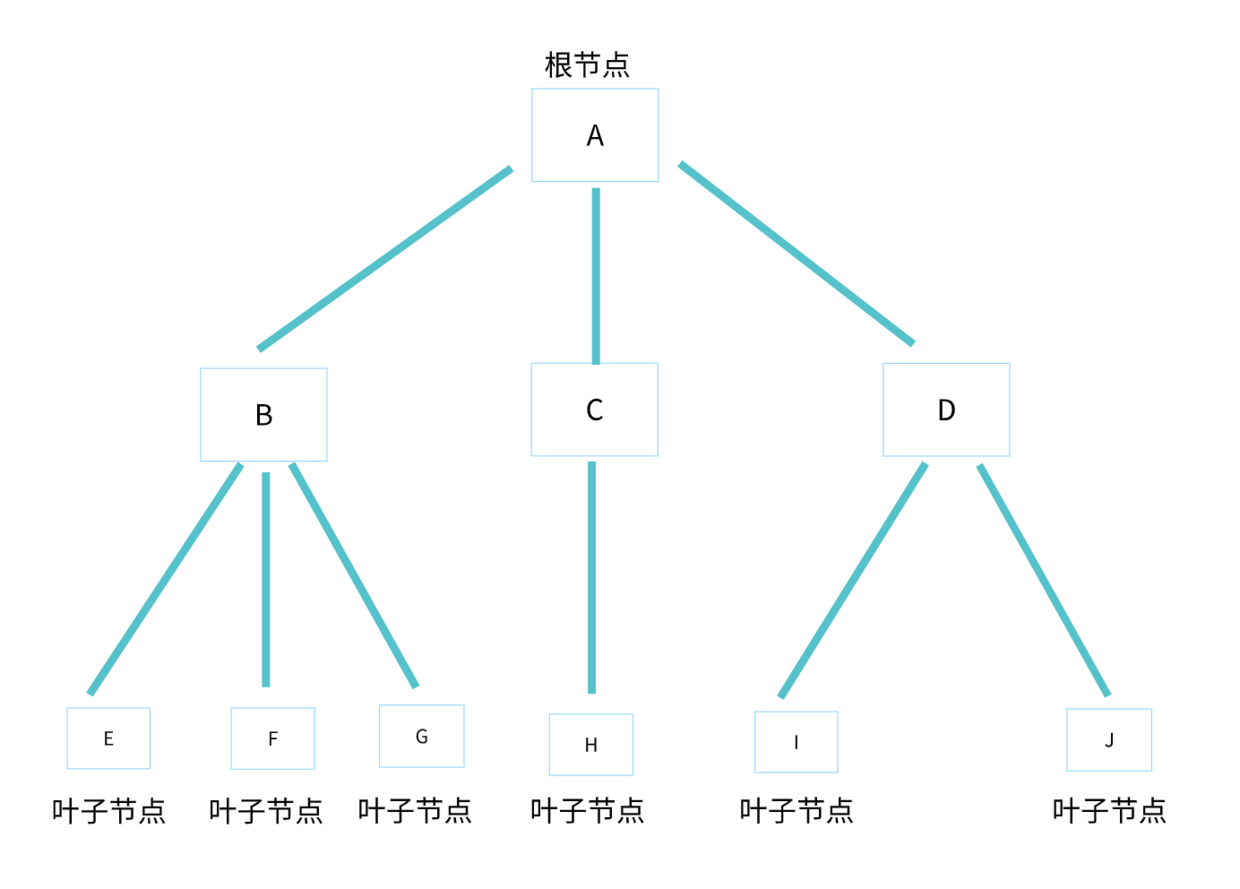
树的数据结构就像我们生活中的真实的树,只不过是倒过来的形状。
术语定义
- 节点:树中的每个元素称为节点,如 A、B、C、D、E、F、G、H、I、J。
- 父节点:指向子节点的节点,如 A。
- 子节点:被父节点指向的节点,如 A 的孩子 B、C、D。
- 父子关系:相邻两节点的连线,称为父子关系,如 A 与 B,C 与 H,D 与 J。
- 根节点:没有父节点的节点,如 A。
- 叶子节点:没有子节点的节点,如 E、F、G、H、I、J。
- 兄弟节点:具有相同父节点的多个节点称为兄弟节点,如 B、C、D。
- 节点的高度:节点到叶子节点的
最长路径所包含的边数。 - 节点的深度:根节点到节点的路径所包含的边数。
- 节点层数:节点的深度 +1(根节点的层数是 1 )。
- 树的高度:等于根节点的高度。
- 森林: n 棵互不相交的树的集合。

高度是从下往上度量,比如一个人的身高 180cm ,起点就是从 0 开始的。
深度是从上往下度量,比如泳池的深度 180cm ,起点也是从 0 开始的。
高度和深度是带有度字的,都是从 0 开始计数的。
而层数的计算,是和我们平时的楼层的计算是一样的,最底下那层是第 1 层,是从 1 开始计数的,所以根节点位于第 1 层,其他子节点依次加 1。
二叉树分类
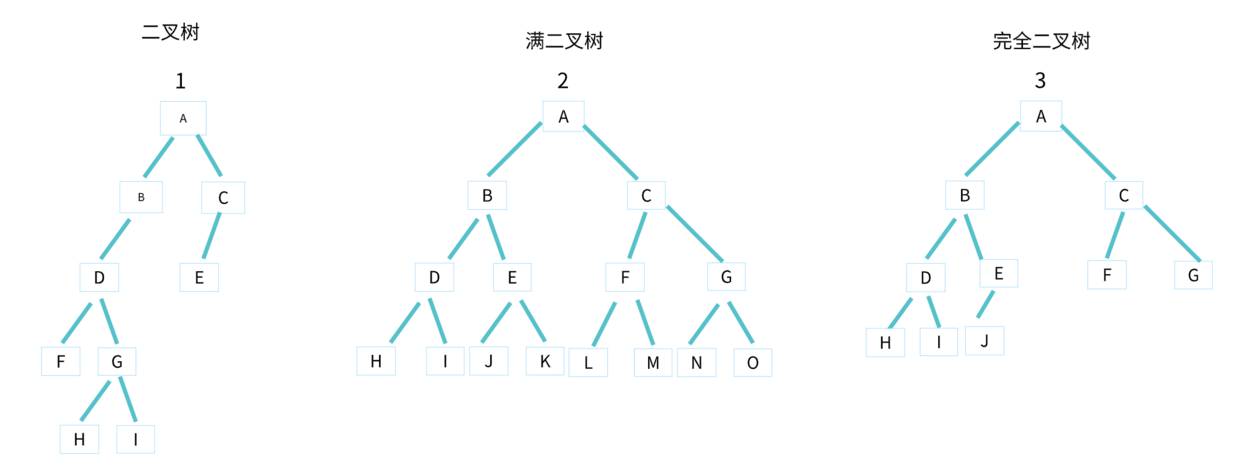
二叉树
- 每个节点
最多只有2 个子节点的树,这两个节点分别是左子节点和右子节点。如上图中的 1、 2、3。
不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。以此类推,自己想四叉树、八叉树的结构图。
满二叉树
- 一种特殊的二叉树,除了叶子节点外,每个节点
都有左右两个子节点,这种二叉树叫做满二叉树。如上图中的 2。
完全二叉树
- 一种特殊的二叉树,叶子节点都在最底下两层,最后一层叶子节都靠
左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树。如上图的 3。
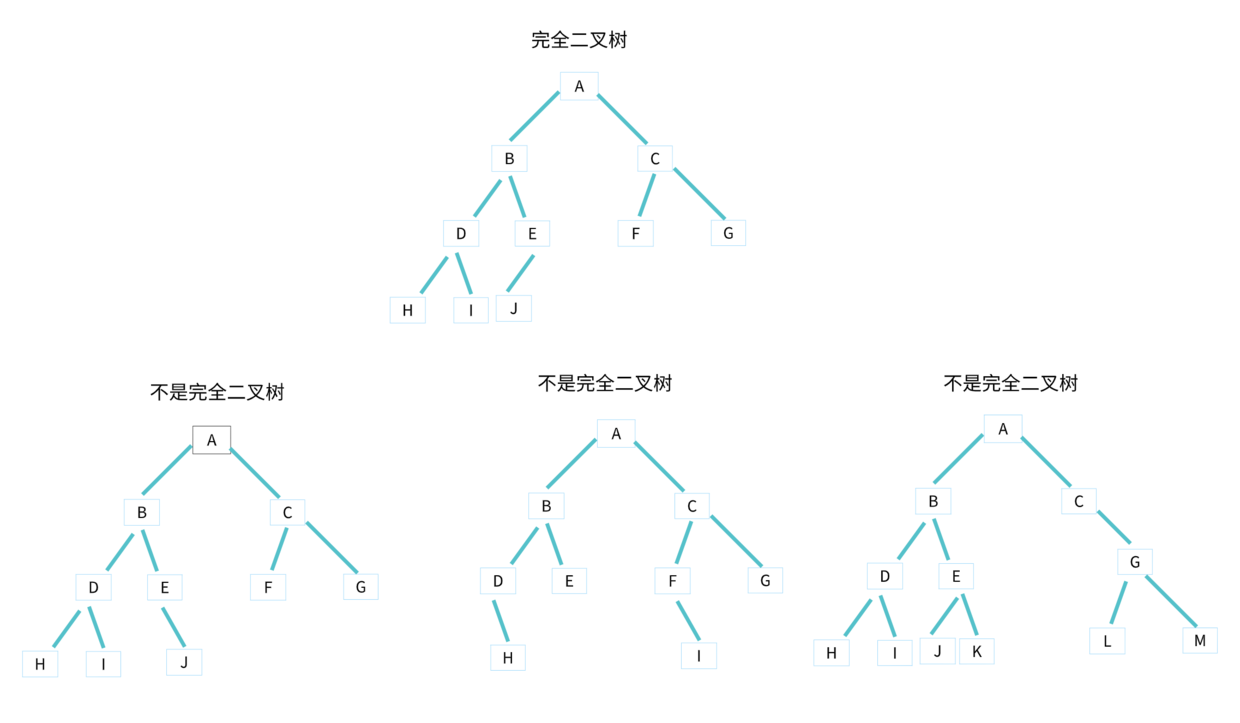
完全二叉树与不是完全二叉树的区分比较难,所以对比下图看看。
堆
之前的文章 栈内存与堆内存 、浅拷贝与深拷贝 中有说到:JavaScript 中的引用类型(如对象、数组、函数等)是保存在堆内存中的对象,值大小不固定,栈内存中存放的该对象的访问地址指向堆内存中的对象,JavaScript 不允许直接访问堆内存中的位置,因此操作对象时,实际操作对象的引用。
那么堆到底是什么呢 ?其数据结构又是怎样的呢 ?
堆其实是一种特殊的树。只要满足这两点,它就是一个堆。
- 堆是一个完全二叉树。
完全二叉树:除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列。 - 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
也可以说:堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值。这两种表述是等价的。
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作大顶堆。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作小顶堆。
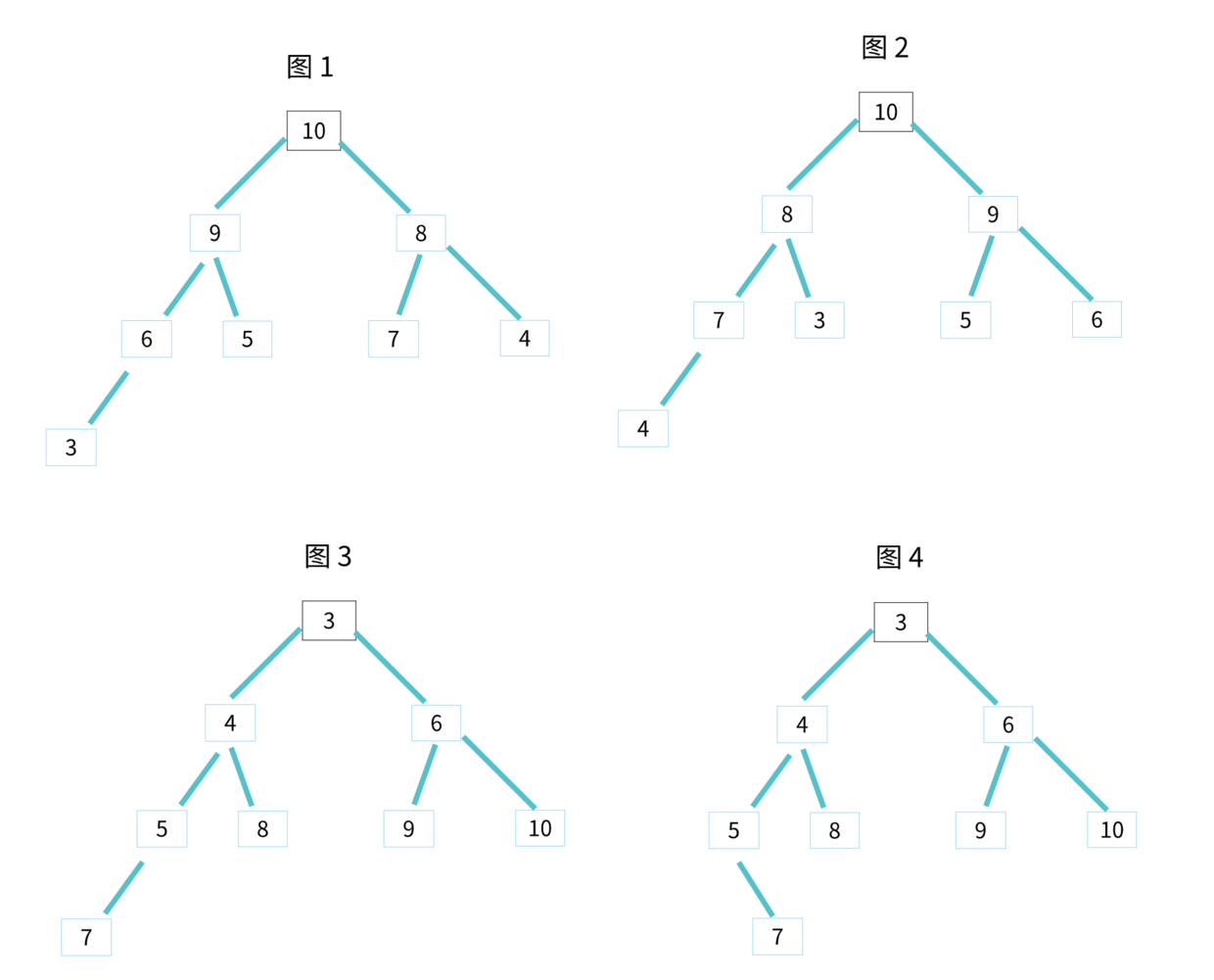
其中图 1 和 图 2 是大顶堆,图 3 是小顶堆,图 4 不是堆。除此之外,从图中还可以看出来,对于同一组数据,我们可以构建多种不同形态的堆。