五、SVM求解实例

　　上面其实已经得出最终的表达式了，下面我们会根据一些具体的点来求解α的值。数据：3个点，其中正例 X₁(3,3) ，X₂(4,3) ，负例X₃(1,1) 如下图所示

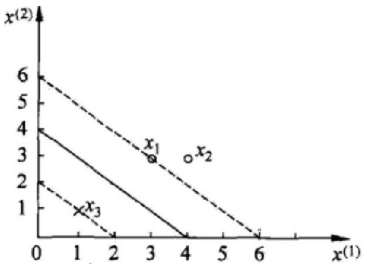
　　我们需要求解下式的极小值

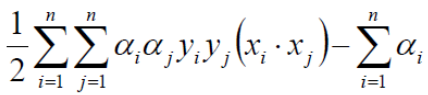
　　注意约束条件（在这里不要忘记了y_i代表的是数据的类别，+1代表正例，-1代表负例）

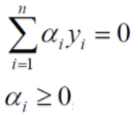
　　代入数据，通过化简可以得到如下约束条件的表达式。

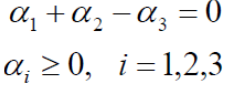
　　将数据代入上式得到

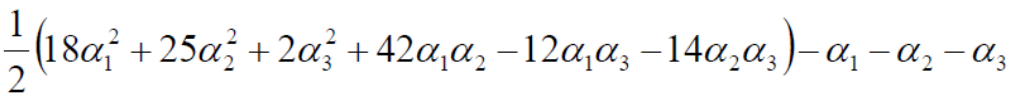
　　由于α₁+α₂-α₃=0 -> α₁+α₂=α₃： 化简可得：

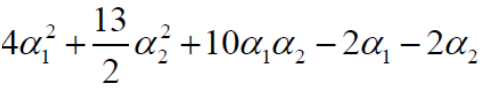
　　分别对α₁和α₂求偏导，偏导等于0可得： α₁=1.5，α₂=-1（并不满足约束条件α_i >= 0，i=1,2,3 ）所以这时求出来的α的值是无效的，那这个时候α的解应在边界上，也就是说要么α₁=0，要么α₂=0，再代入上式然后求偏导看下

　　(这儿经过我的计算发现α₂似乎等于正的2/13，应该是教程有些小问题，猜测可能是上式由α₁+α₂=α₃化简这儿出了点小问题，但是对于答案似乎影响不大) ，所以经过计算最小值在(0.25,0,0.25)处取得 。

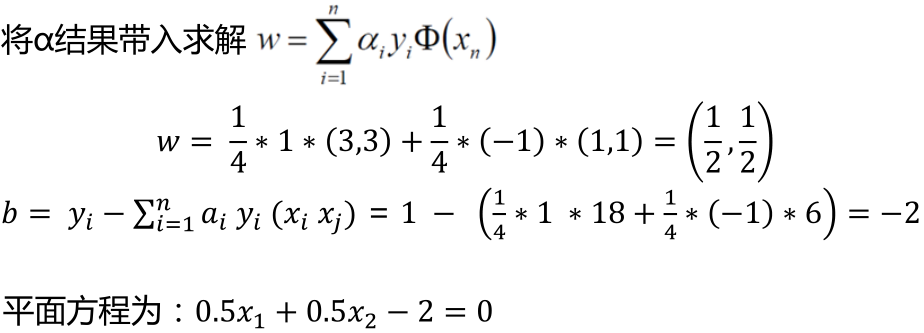
　　上面的平面方程其实就是代表直线方程，也就是决策边界的方程。

六、支持向量机？

　　为什么会取支持向量机这样一个名字呢？

　　我们可以发现决策边界只与α不等零的有关系，因为w=α_iy_i的累加和，所以α为0的点不起作用。

　　可以得出所有边界上的点α值必然不等于0，也称作支持向量，所有非边界上的点α值必等于0，也称作非支持向量。支持向量机中的机指的就是决策边界，而决策边界就是由支持向量所支撑的，支持向量就是边界点α值不为0的点，决定边界。如下图所示当取60个样本点和120个样本点时，只要添加的不是边界上的样本点，那么决策边界就是不变的。

七、软间隔 

　　软间隔：有时候数据中有一些噪音点，如果考虑它们的话那咱们的决策边界线就不太好界定了，之前的方法要求把两类点完全分得开，这个要求有点过于严格了，我们来放松一点！

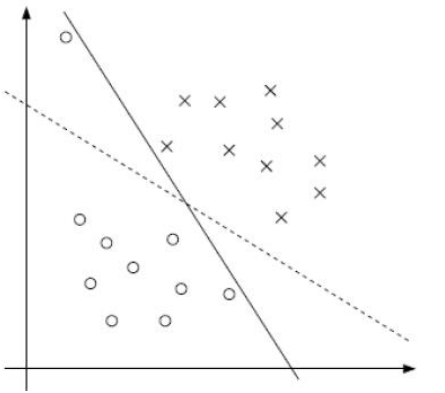
　　为了解决该问题，引入松弛因子ξ

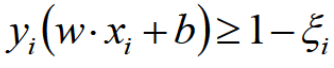
　　那我们就有了新的目标函数：

　　当C趋近于很大时，要使得整体很小的话，那么意味着松弛因子ξ就会很小，那就意味着分类严格不能有错误。当C趋近于很小时，要使得整体很小的话，那就意味着松弛因子ξ可以稍微大一些，那就意味着可以有更大的错误容忍。C是我们实际在编程中需要指定的一个参数！下面是多了一个松弛因子ξ下的拉格朗日乘子法，基本上和上面差不多的。

八、核变换

　　将低维不可分问题(一般就是非线性支持向量机问题)映射为空间中的高维可分问题，这就是核变换。上面我们提到了这个函数Φ(X) ，那这个函数的意思就是代表一种核变换的方法。如下图在二维平面下分类很困难，但是如果将数据映射到3为空间，那这样就很好划分了。

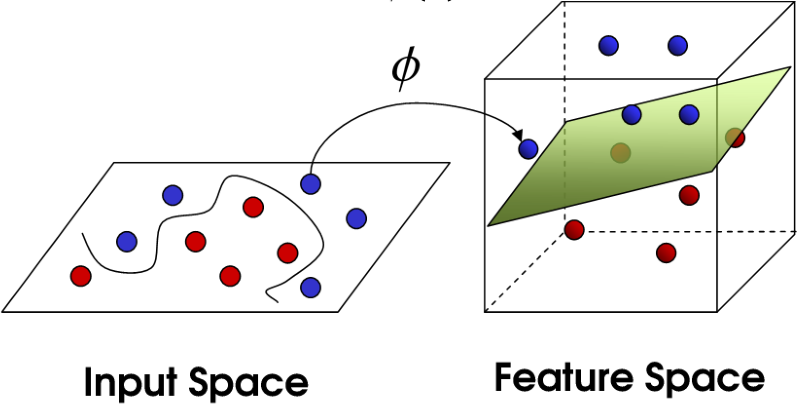
　　还是先从一个小例子来阐述问题。假设我们有俩个数据，x=(x₁,x₂,x₃)，y=(y₁,y₂,y₂)，此时在3D空间已经不能对其进行线性划分了，那么我们通过一个函数Φ(X)将数据映射到更高维的空间，比如9维的话，那么f(x)=(x₁x₁,x₁x₂,x₁x₃,x₂x₁,x₂x₂,x₂x₃,x