目录

@

一、平衡二叉树定义

平衡二叉树又称AVL树。它可以是一颗空树，或者具有以下性质的二叉排序树：它的左子树和右子树的高度之差(平衡因子)的绝对值不超过1且它的左子树和右子树都是一颗平衡二叉树。

从上面简单的定义我们可以得出几个重要的信息：

• 平衡二叉树又称AVL树
• 平衡二叉树必须是二叉排序树
• 每个节点的左子树和右子树的高度差至多为1。

在定义中提到了树的高度和深度，我敢肯定有很多读者一定对树的高度和深度有所误解！最可爱的误解就是树的高度和深度没有区别，认为树的高度就是深度。宜春就忍不了了，必须得哔哔几句...

树的高度和深度本质区别：深度是从根节点数到它的叶节点，高度是从叶节点数到它的根节点。

二叉树的深度是从根节点开始自顶向下逐层累加的；而二叉树高度是从叶节点开始自底向上逐层累加的。虽然树的深度和高度一样，但是具体到树的某个节点，其深度和高度是不一样的。

其次就是对树的高度和深度是从1数起，还是从0数起。当然我也有自己的答案，但是众说纷纭，博主就不说其对与错了，就不多哔哔了。但是我还是比较认同这张图的观点：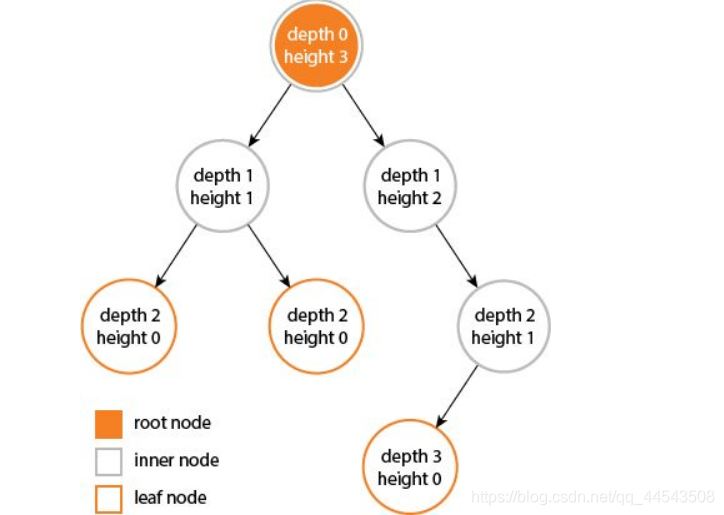
可参考：

三、平衡因子

不多哔哔，平衡因子 = 左子树深度/高度 - 右子树深度/高度

对于上图平衡二叉树而言：
5的结点平衡因子就是 3 - 2 = 1；
2的结点平衡因子就是 1 - 2 = -1；
4的结点平衡因子就是 1 - 0 = 1；
6的结点平衡因子就是 0 - 1 = -1；

对于上图非平衡二叉树而言：
3 的结点平衡因子就是 2 - 4 = -2；
1 的结点平衡因子就是 0 - 1 = -1；
4 的结点平衡因子就是 0 - 3 = -3；
5 的结点平衡因子就是 0 - 2 = -2；
6 的结点平衡因子就是 0 - 1 = -1；

特别注意：叶子结点平衡因子都是为 0

四、如何保持平衡二叉树平衡？

由于普通的二叉查找树会容易失去”平衡“，极端情况下，二叉查找树会退化成线性的链表，导致插入和查找的复杂度下降到 O(n) ，所以，这也是平衡二叉树设计的初衷。那么平衡二叉树如何保持”平衡“呢？

不难看出平衡二叉树是一棵高度平衡的二叉查找树。所以，要构建跟维系一棵平衡二叉树就比普通的二叉树要复杂的多。在构建一棵平衡二叉树的过程中，当有新的节点要插入时，检查是否因插入后而破坏了树的平衡，如果是，则需要做旋转去改变树的结构。关于旋转，我相信使用文字描述是很难表达清楚的，还是得靠经典的两个图来理解最好不过了！不要不信噢，当然你可以尝试读下文字描述左旋：

左旋简单来说就是将节点的右支往左拉，右子节点变成父节点，并把晋升之后多余的左子节点出让给降级节点的右子节点。

相信你已经晕了。当然可以试着看看下面的经典动图理解！

左旋：

==试着用动态和下面的左旋结果图分析分析，想象一下，估计分分钟明白左旋！！！==

 //左旋转方法代码     private void leftRotate() {         //创建新的结点，以当前根结点的值         Node newNode = new Node(value);         //把新的结点的左子树设置成当前结点的左子树         newNode.left = left;         //把新的结点的右子树设置成带你过去结点的右子树的左子树         newNode.right = right.left;         //把当前结点的值替换成右子结点的值         value = right.value;         //把当前结点的右子树设置成当前结点右子树的右子树         right = right.right;